Logistic Regression Machine Learning

Aug 17, 2024

logistic regression machine learning

Logistic regression is a fundamental concept in machine learning, widely used for binary classification tasks. It predicts the probability that a given input belongs to a particular class, making it an essential tool for data scientists and engineers. This blog post will explore logistic regression in detail, providing insights into its workings, applications, advantages, and code snippets to help you implement it effectively.

Understanding Logistic Regression

What is Logistic Regression?

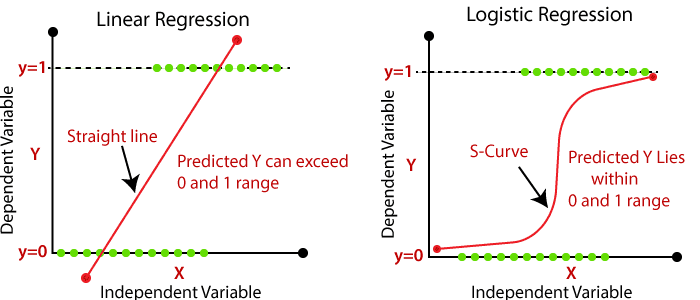
Logistic regression is a statistical method used for binary classification problems. Unlike linear regression, which predicts continuous values, logistic regression predicts discrete outcomes, typically represented as 0 or 1. It estimates the probability that a given input belongs to a specific class, using a logistic function to model the relationship between the independent variables and the dependent binary variable.

The Logistic Function

The logistic function, also known as the sigmoid function, is defined as:

f(z)=11+e−z​

where zz is a linear combination of the input features. This function maps any real-valued number into the range of 0 to 1, making it suitable for modeling probabilities.

The Logistic Regression Model

In logistic regression, the relationship between the independent variables XX and the dependent variable YY is modeled as:

P(Y=1∣X)=11+e−(β0+β1X1+β2X2+...+βnXn)

Here, β0β0​ is the intercept, and β1,β2,...,βnβ1​,β2​,...,βn​ are the coefficients for each independent variable X1,X2,...,XnX1​,X2​,...,Xn​.

Key Terms in Logistic Regression

  • Binary Classification: A classification task where the output can take one of two possible values.

  • Log Odds: The logarithm of the odds ratio, which is the ratio of the probability of the event occurring to the probability of it not occurring.

  • Maximum Likelihood Estimation (MLE): A method used to estimate the coefficients of the logistic regression model by maximizing the likelihood function.

Applications of Logistic Regression

Logistic regression is versatile and can be applied in various fields, including:

  • Healthcare: Predicting the likelihood of diseases based on patient data.

  • Finance: Assessing the risk of loan defaults.

  • Marketing: Classifying customer responses to campaigns.

  • Spam Detection: Identifying whether an email is spam or not.

Advantages of Logistic Regression

  1. Simplicity: Logistic regression is easy to implement and interpret.

  2. Efficiency: It requires less computational power compared to more complex algorithms.

  3. Probabilistic Output: It provides probabilities for class membership, allowing for nuanced decision-making.

Implementing Logistic Regression in Python

To implement logistic regression, we can use popular libraries such as scikit-learn. Below is a step-by-step guide along with code snippets.

Step 1: Import Libraries

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, confusion_matrix

Step 2: Load the Dataset

For this example, we will use a hypothetical dataset containing features related to loan applications.

# Load dataset
data = pd.read_csv('loan_data.csv')

# Display the first few rows
print(data.head())

Step 3: Preprocess the Data

Ensure the data is clean and ready for modeling.

# Handle missing values
data.fillna(method='ffill', inplace=True)

# Convert categorical variables to dummy variables
data = pd.get_dummies(data, drop_first=True)

Step 4: Split the Data

Divide the dataset into training and testing sets.

X = data.drop('default', axis=1)  # Features
y = data['default']  # Target variable

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Step 5: Train the Model

Fit the logistic regression model to the training data.

model = LogisticRegression()
model.fit(X_train, y_train)

Step 6: Make Predictions

Use the trained model to make predictions on the test set.

y_pred = model.predict(X_test)

Step 7: Evaluate the Model

Assess the model's performance using accuracy and confusion matrix.

accuracy = accuracy_score(y_test, y_pred)
conf_matrix = confusion_matrix(y_test, y_pred)

print(f'Accuracy: {accuracy}')
print(f'Confusion Matrix:\n{conf_matrix}')

Challenges and Limitations

While logistic regression is powerful, it has limitations:

  • Linear Decision Boundary: It assumes a linear relationship between the features and the log odds of the outcome, which may not hold true for all datasets.

  • Sensitive to Outliers: Logistic regression can be affected by outliers, potentially skewing the results.

  • Multicollinearity: High correlation between independent variables can impact the stability of the coefficient estimates.

Conclusion

Logistic regression is a fundamental technique in machine learning, particularly for binary classification tasks. Its simplicity, efficiency, and interpretability make it a popular choice among data scientists. By understanding its mechanics and implementing it using tools like Python, you can leverage logistic regression to solve various real-world problems effectively.