Machine Learning Regression Algorithms: A Comprehensive Guide

Aug 16, 2024

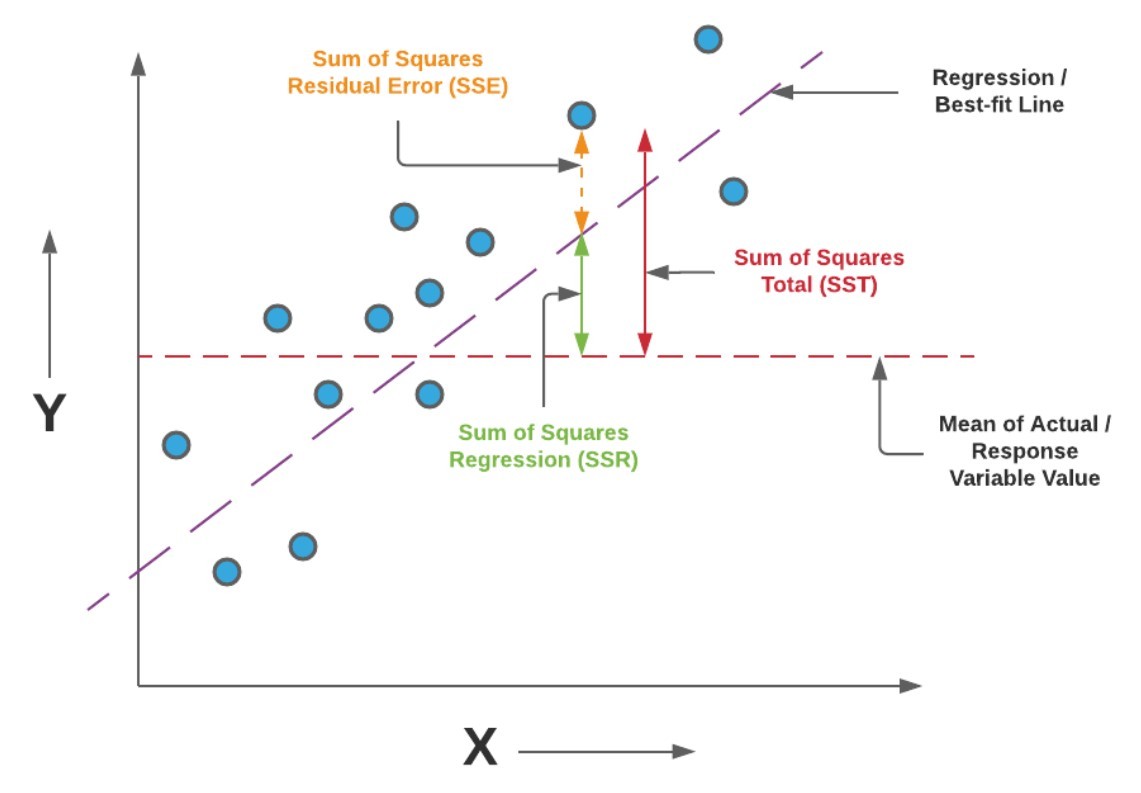
Machine learning regression algorithms are essential tools in the field of data science, allowing practitioners to predict continuous outcomes based on input features. This blog post will delve into the various types of regression algorithms, their applications, and provide code snippets to illustrate how they can be implemented in Python. By the end of this guide, you will have a solid understanding of machine learning regression algorithms and how to apply them effectively.

What is Regression in Machine Learning?

Regression is a type of supervised learning where the goal is to predict a continuous output variable based on one or more input features. Unlike classification algorithms, which categorize data points into discrete classes, regression algorithms estimate relationships between variables, allowing for predictions of numerical values such as prices, temperatures, or sales figures.

Key Concepts in Regression

Before diving into specific algorithms, it's important to understand some key concepts:

Dependent Variable: The outcome variable that we are trying to predict.
Independent Variables: The features or inputs used to make predictions.
Cost Function: A measure of how well the model's predictions match the actual data. Common cost functions include Mean Squared Error (MSE) and Mean Absolute Error (MAE).
Overfitting: A situation where the model learns the training data too well, including noise and outliers, leading to poor performance on unseen data.

Popular Machine Learning Regression Algorithms

Here are some of the most widely used regression algorithms in machine learning:

1. Linear Regression

Linear regression is the simplest and most commonly used regression algorithm. It assumes a linear relationship between the dependent and independent variables.

Mathematical Representation:

y=β0+β1x1+β2x2+...+βnxn+ϵ

Where:

yy is the predicted value,
β0β0 is the intercept,
β1,β2,...,βnβ1,β2,...,βn are the coefficients,
x1,x2,...,xnx1,x2,...,xn are the independent variables,
ϵϵ is the error term.

Python Implementation:

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

# Load dataset
data = pd.read_csv('data.csv')
X = data[['feature1', 'feature2']]
y = data['target']

# Split the data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Create and train the model
model = LinearRegression()
model.fit(X_train, y_train)

# Make predictions
predictions = model.predict(X_test)

# Evaluate the model
mse = mean_squared_error(y_test, predictions)
print(f'Mean Squared Error: {mse}')

2. Ridge Regression

Ridge regression is a type of linear regression that includes a regularization term to prevent overfitting. It adds a penalty equal to the square of the magnitude of coefficients.Cost Function:

J(β)=∑i=1n(yi−y^i)2+λ∑j=1pβj2

Whereλλis the regularization parameter.

Python Implementation:

from sklearn.linear_model import Ridge

# Create and train the model
ridge_model = Ridge(alpha=1.0)
ridge_model.fit(X_train, y_train)

# Make predictions
ridge_predictions = ridge_model.predict(X_test)

# Evaluate the model
ridge_mse = mean_squared_error(y_test, ridge_predictions)
print(f'Ridge Mean Squared Error: {ridge_mse}')

3. Lasso Regression

Lasso regression is similar to ridge regression but uses L1 regularization, which can shrink some coefficients to zero, effectively performing variable selection.

Cost Function:

J(β)=∑i=1n(yi−y^i)2+λ∑j=1p∣βj∣

Python Implementation:

from sklearn.linear_model import Lasso

# Create and train the model
lasso_model = Lasso(alpha=0.1)
lasso_model.fit(X_train, y_train)

# Make predictions
lasso_predictions = lasso_model.predict(X_test)

# Evaluate the model
lasso_mse = mean_squared_error(y_test, lasso_predictions)
print(f'Lasso Mean Squared Error: {lasso_mse}')

4. Polynomial Regression

Polynomial regression is used when the relationship between the independent variable and the dependent variable is nonlinear. It involves transforming the input features into polynomial features.

Python Implementation:

from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import make_pipeline

# Create polynomial regression model
degree = 2
polyreg_model = make_pipeline(PolynomialFeatures(degree), LinearRegression())
polyreg_model.fit(X_train, y_train)

# Make predictions
polyreg_predictions = polyreg_model.predict(X_test)

# Evaluate the model
polyreg_mse = mean_squared_error(y_test, polyreg_predictions)
print(f'Polynomial Regression Mean Squared Error: {polyreg_mse}')

Choosing the Right Regression Algorithm

Selecting the appropriate regression algorithm depends on several factors:

Nature of the Data: If the relationship between the features and target variable is linear, linear regression may suffice. For non-linear relationships, consider polynomial regression or decision tree regression.
Number of Features: If you have many features, regularized models like Ridge or Lasso can help prevent overfitting.
Interpretability: Linear models are easier to interpret compared to more complex models like decision trees or SVR.
Performance: Experiment with different algorithms and evaluate their performance using metrics like MSE or R-squared.

Conclusion

Machine learning regression algorithms are powerful tools for predicting continuous outcomes based on input data. By understanding the various types of regression algorithms, their mathematical foundations, and how to implement them in Python, you can effectively tackle a wide range of predictive modeling tasks.

As you explore these algorithms, remember to consider the specific characteristics of your data and the goals of your analysis. With practice, you'll be able to select and apply the most suitable regression algorithm for your machine learning projects.