Understanding Ridge Regression: A Comprehensive Guide

Aug 17, 2024

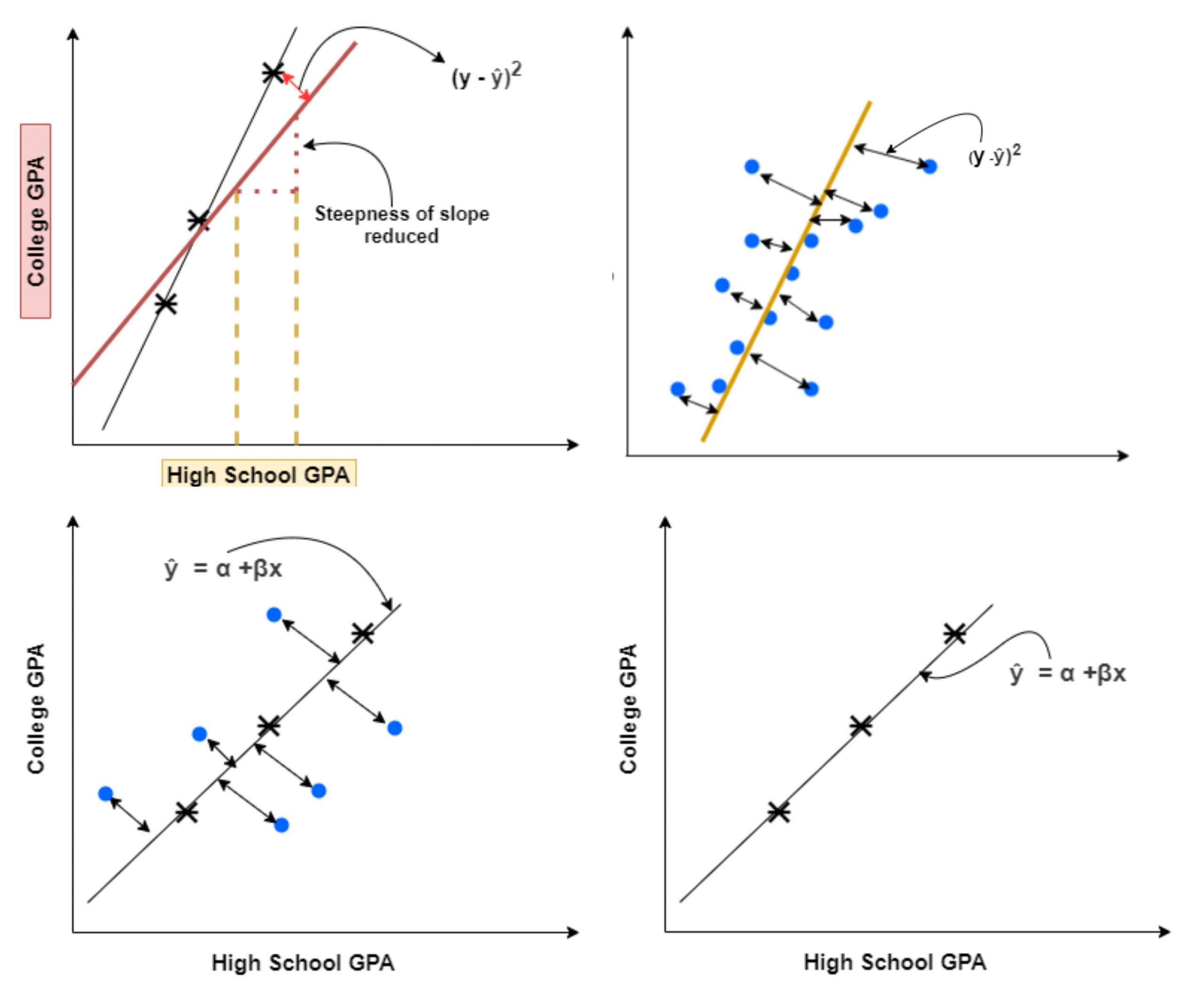
Understanding Ridge Regression: A Comprehensive Guide

Ridge regression is a powerful statistical technique used in machine learning and data analysis to address the challenges posed by multicollinearity among predictor variables. This blog post delves into the intricacies of ridge regression, its mathematical foundation, implementation in Python, and its advantages and disadvantages. By the end, you will have a thorough understanding of ridge regression and how to apply it effectively in your predictive modeling tasks.

What is Ridge Regression?

Ridge regression is a type of linear regression that incorporates a regularization term to improve the model's stability and predictive performance. Traditional linear regression can struggle when predictor variables are highly correlated, leading to unreliable coefficient estimates. Ridge regression mitigates this issue by adding a penalty to the loss function, which discourages large coefficients and helps stabilize the model.

The Mathematical Foundation

The cost function for ridge regression is defined as:

J(β)=MSE(β)+λ∑j=1pβj2

Where:

  • J(β)J(β) is the cost function to minimize.

  • MSE(β)MSE(β) is the mean squared error of the model.

  • λλ (lambda) is the regularization parameter that controls the strength of the penalty.

  • βjβj​ are the coefficients of the predictor variables.

The addition of the term λ∑j=1pβj2​ (the L2 penalty) helps to shrink the coefficients towards zero, thereby reducing the model complexity and improving generalization to unseen data.

The Role of the Regularization Parameter

The regularization parameter λλ plays a crucial role in ridge regression. It determines the amount of shrinkage applied to the coefficients:

  • High λλ: More shrinkage, leading to smaller coefficients. This can reduce variance but may introduce bias.

  • Low λλ: Less shrinkage, allowing coefficients to take larger values, which can lead to overfitting.

Choosing the optimal λλ is essential and is often done using techniques such as cross-validation.

Implementing Ridge Regression in Python

To implement ridge regression in Python, we can use the scikit-learn library. Below is a step-by-step guide to setting up and running a ridge regression model.

Step 1: Import Required Libraries

import numpy as np
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Ridge
from sklearn.metrics import mean_squared_error

Step 2: Prepare the Data

Load your dataset and split it into training and testing sets.

# Load dataset
data = pd.read_csv('your_dataset.csv')

# Define features and target variable
X = data.drop('target', axis=1)
y = data['target']

# Split the data
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Step 3: Standardize the Data

Standardization is crucial for ridge regression to ensure that all features contribute equally to the distance calculations.

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

Step 4: Fit the Ridge Regression Model

Create and fit the ridge regression model.

# Create a ridge regression model
ridge_model = Ridge(alpha=1.0)  # You can adjust alpha (lambda) as needed

# Fit the model
ridge_model.fit(X_train_scaled, y_train)

Step 5: Make Predictions and Evaluate the Model

After fitting the model, you can make predictions and evaluate its performance.

# Make predictions
y_pred = ridge_model.predict(X_test_scaled)

# Calculate the mean squared error
mse = mean_squared_error(y_test, y_pred)
print(f'Mean Squared Error: {mse}')

Advantages of Ridge Regression

  1. Handles Multicollinearity: Ridge regression effectively reduces the influence of correlated features, making it suitable for datasets with high collinearity.

  2. Improves Prediction Accuracy: By adding a penalty term, ridge regression enhances the model's ability to generalize to new data.

  3. Reduces Overfitting: The regularization term helps prevent the model from fitting noise in the training data, leading to better performance on unseen data.

  4. Stability: Ridge regression provides more stable and reliable estimates of coefficients, particularly in the presence of noisy data.

Disadvantages of Ridge Regression

  1. Limited Feature Selection: Unlike Lasso regression, ridge regression does not perform feature selection. It retains all features, which may not be ideal in some scenarios.

  2. Sensitivity to Hyperparameters: The effectiveness of ridge regression is highly dependent on the choice of the regularization parameter λλ. Careful tuning is required to achieve optimal results.

  3. Reduced Interpretability: The presence of all features in the model can make it harder to interpret the results compared to models that select a subset of features.

Conclusion

Ridge regression is a vital technique in the toolkit of data scientists and statisticians, particularly when dealing with multicollinearity and overfitting in predictive models. By incorporating a regularization term, ridge regression enhances the stability and accuracy of linear regression models, making it a preferred choice in many scenarios.

Understanding the mathematical foundations, implementation, and advantages of ridge regression allows practitioners to apply this technique effectively. Whether you are working on high-dimensional datasets or seeking to improve your model's predictive performance, ridge regression offers a robust solution.